Viewing Gene Expression Distributions

A great deal of quality-control information comes from the alignment step itself. Here we are concerned with how the data looks as an ensemble. Many methods are particularly concerned with the dispersion of genes.

In this notebook we demonstrate the plotting utilities provided by gsforge to examine such distributions.

Set up the notebook

import itertools
import holoviews as hv
import numpy as np
import xarray as xr
import GSForge as gsf
hv.extension('bokeh')

import matplotlib.pyplot as plt
import colorcet as cc
from datashader.mpl_ext import dsshow, alpha_colormap
import datashader
from functools import partial
import seaborn as sns
from mpl_toolkits.axes_grid1 import make_axes_locatable

Declare used paths

# OS-independent path management.
from os import  environ
from pathlib import Path

OSF_PATH = Path(environ.get("GSFORGE_DEMO_DATA", default="~/GSForge_demo_data/")).expanduser().joinpath("osfstorage", "oryza_sativa")
NORMED_GEM_PATH = OSF_PATH.joinpath("AnnotatedGEMs", "oryza_sativa_hisat2_normed.nc")

Load an AnnotatedGEM

agem = gsf.AnnotatedGEM(NORMED_GEM_PATH)
agem

<GSForge.AnnotatedGEM>
Name: Oryza sativa
Selected GEM Variable: 'counts'
    Gene   55986
    Sample 475

View available count arrays

agem.count_array_names

['counts',
 'TPM_counts',
 'uq_raw_counts',
 'uq_tpm_counts',
 'quantile_counts',
 'tmm_counts']

gsf.plots.gem.GenewiseAggregateScatter(
    agem,
    count_variable='counts',
    x_axis_selector='mean',
    y_axis_selector='variance',
    count_transform=lambda c: np.log2(c + 1),
    datashade=True,
    dynspread=True,
)

Recall that all gsforge plotting operations allow use of the Interface data selection pipeline.

In this case we can select another count array and view the normalized distributions.

gsf.plots.gem.GenewiseAggregateScatter(
    agem,
    count_variable='TPM_counts',
    x_axis_selector='mean',
    y_axis_selector='variance',
    count_transform=lambda c: np.log2(c + 1),
    datashade=True,
    dynspread=True,
)

# for count_var, y_axis in itertools.product(agem.count_array_names, ['variance', 'fano', 'cv_squared']):

#     plot = gsf.plots.gem.GenewiseAggregateScatter(
#         agem,
#         count_variable=count_var,
#         x_axis_selector='mean',
#         y_axis_selector=y_axis,
#         axis_transform=('log 2', lambda ds: np.log2(ds.where(ds > 0))),
#         datashade=True,
#         dynspread=True,
#     )

    # hv.save(plot, f'figures/genewise_aggs/gw_agg_{count_var}_log2_mean_vs_log2_{y_axis}.png', dpi=300, toolbar=None)

For some reason the adjoint png files produced have extra white space. We can remove that with a solution from github

# from PIL import Image
# from PIL import ImageOps

# padding = 5
# padding = np.asarray([-1*padding, -1*padding, padding, padding])

# for figure in Path('figures/genewise_aggs').glob('gw_agg_*.png'):
    
#     image = Image.open(figure)
#     image.load()
#     imageSize = image.size

#     # remove alpha channel
#     invert_im = image.convert("RGB")

#     # invert image (so that white is 0)
#     invert_im = ImageOps.invert(invert_im)
#     imageBox = invert_im.getbbox()
#     imageBox = tuple(np.asarray(imageBox)+padding)

#     cropped = image.crop(imageBox)
#     cropped.save(figure)

Grouped-Sample Covariance

These plotting functions can take a few minutes to complete.

treatment_labels = agem.data['treatment'].to_series().unique()
treatment_labels

array(['CONTROL', 'HEAT', 'RECOV_HEAT', 'DROUGHT', 'RECOV_DROUGHT'],
      dtype=object)

# %%time
# for group_a, group_b in itertools.combinations(treatment_labels, 2):
#     plot =  gsf.plots.gem.GroupedGeneCovariance(agem, group_variable='treatment', 
#                                                 x_group_label=group_a, y_group_label=group_b,
#                                                 count_transform=lambda c: np.log(c + 0.25)
#                                                ).opts(size=0.75, width=300, height=300)
#     hv.save(plot, f'figures/grouped_covariance/covariance_{group_a}_vs_{group_b}.png', 'png')

Sample-wise Distributions

These plotting func tions can take a few minutes to complete.

Kernel Density Estimates

# %%time
# for count_var, hue in itertools.product(['counts'], [None]):
#     plot = gsf.plots.gem.SamplewiseDistributions(agem, count_variable=count_var, hue_key=hue, 
#                                                  datashade=False)#.opts(width=300, height=300)
#     hv.save(plot, f'figures/kde/samplewise_kde_{count_var}_{hue}.png', toolbar=None)

Empirical Cumulative Distribution

# %%time
# for count_var, hue in itertools.product(agem.count_array_names[:-1], [None, 'treatment', 'genotype']):
#     plot = gsf.plots.gem.EmpiricalCumulativeDistribution(agem, hue_key=hue, count_variable=count_var, datashade=True)
#     hv.save(plot, f'figures/ecdf/ECDF_{count_var}_{hue}.png', dpi=300, toolbar=None)

plt.style.use('default')
plt.rcParams.update({'font.size': 11, 'font.family': 'serif'})

log_counts, _ = gsf.get_gem_data(agem, count_transform=lambda c: np.log2(c + 1), count_variable='TPM_counts')
data = xr.Dataset({
    "mean": np.mean(log_counts, axis=0),
    "variance": np.sqrt(np.var(log_counts, axis=0)),
})
data = data.set_coords(['mean', 'variance'])
hv.operation.datashader.datashade(
    hv.Points(data, kdims=['mean', 'variance']),
    cmap='inferno', cnorm='log',
).opts(bgcolor='lightgrey', padding=0.05, width=600, height=400, show_grid=True)

log_counts, _ = gsf.get_gem_data(agem, count_transform=lambda c: np.log2(c + 1))
data = xr.Dataset({
    "mean": np.mean(log_counts, axis=0),
    "variance": np.sqrt(np.var(log_counts, axis=0)),
})
data = data.set_coords(['mean', 'variance'])
hv.operation.datashader.datashade(
    hv.Points(data, kdims=['mean', 'variance']),
    cmap='inferno', cnorm='log',
).opts(bgcolor='lightgrey', padding=0.05, width=600, height=400, show_grid=True)

log_counts, _ = gsf.get_gem_data(agem, count_transform=lambda c: np.log2(c + 1), count_variable='quantile_counts')
data = xr.Dataset({
    "mean": np.mean(log_counts, axis=0),
    "variance": np.sqrt(np.var(log_counts, axis=0)),
})
data = data.set_coords(['mean', 'variance'])
hv.operation.datashader.datashade(
    hv.Points(data, kdims=['mean', 'variance']),
    cmap='inferno', cnorm='log',
).opts(bgcolor='lightgrey', padding=0.05, width=600, height=400, show_grid=True)

/home/tyler/anaconda3/envs/gsfenv/lib/python3.7/site-packages/xarray/core/computation.py:742: RuntimeWarning: invalid value encountered in log2
  result_data = func(*input_data)

log_counts, _ = gsf.get_gem_data(agem, count_transform=lambda c: np.log2(c + 1), count_variable='TPM_counts')
data = xr.Dataset({
    "mean log2 counts": np.mean(log_counts, axis=0),
    "sqrt log2 variance": np.sqrt(np.var(log_counts, axis=0)),
})
data = data.set_coords(['mean log2 counts', 'sqrt log2 variance'])
x_min = data['mean log2 counts'].values.min()
x_max = data['mean log2 counts'].values.max()

y_min = data['sqrt log2 variance'].values.min()
y_max = data['sqrt log2 variance'].values.max()

padding = 0.05
x_pad = (x_max - x_min) * padding
y_pad = (y_max - y_min) * padding

x_min -= x_pad
# x_max += x_pad
x_max = 11.5

y_min -= y_pad
# y_max += y_pad
y_max = 2


fig_inches = 3.5
fig_dpi = 300
fig_pixels = int(fig_inches * fig_dpi)

fig, axScatter = plt.subplots(figsize=(fig_inches, fig_inches), constrained_layout=True, dpi=fig_dpi)

axScatter.scatter(
    data['mean log2 counts'].values,
    data['sqrt log2 variance'].values,
    s=0.5,
    alpha=0.5, 
    marker='.', 
    edgecolors='none', 
)
# dsshow(
#     data, 
#     datashader.Point('mean log2 counts', 'sqrt log2 variance'), 
#     shade_hook=datashader.transfer_functions.dynspread,
#     norm='eq_hist', cmap="Blues", ax=axScatter, 
#     aspect='auto',
#     x_range=(x_min, x_max),
#     y_range=(y_min, y_max),
#     plot_width=fig_pixels,
#     plot_height=fig_pixels,
# );

divider = make_axes_locatable(axScatter)
axHistx = divider.append_axes("top", 0.2*fig_inches, pad=0.15)
axHisty = divider.append_axes("right", 0.2*fig_inches, pad=0.15)

axHistx.xaxis.set_tick_params(labelbottom=False)
axHisty.yaxis.set_tick_params(labelleft=False)

axHistx.set_xlim(x_min, x_max)
axHisty.set_ylim(y_min, y_max)

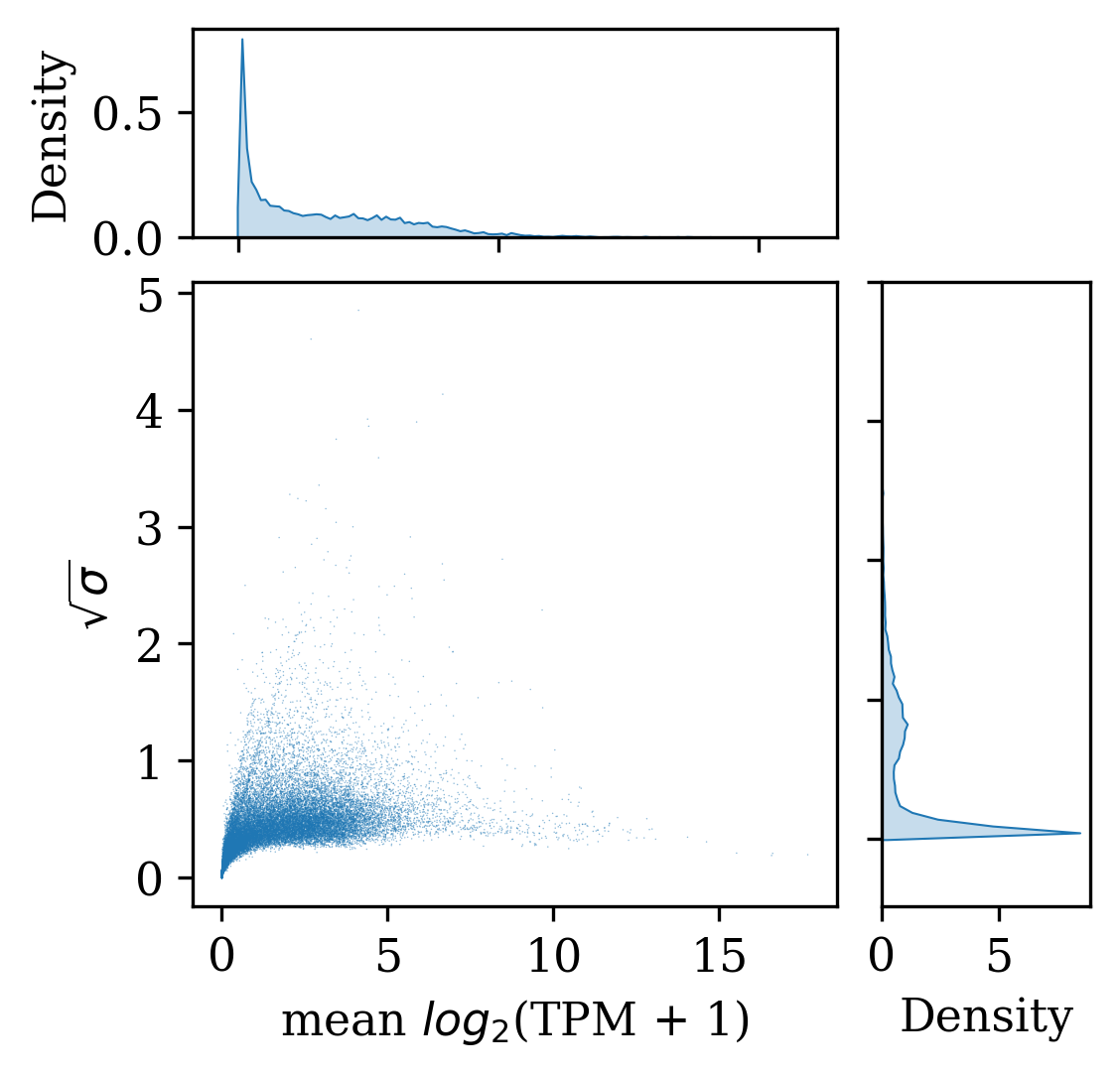
sns.kdeplot(data["mean log2 counts"].values, ax=axHistx, linewidth=0.5, shade=True, bw_adjust=0.05)
sns.kdeplot(y=data["sqrt log2 variance"].values, ax=axHisty, linewidth=0.5, shade=True, bw_adjust=0.05)

axScatter.set(xlabel='mean $log_2$(TPM + 1)', ylabel='$\sqrt{\sigma}$');

[Text(0.5, 0, 'mean $log_2$(TPM + 1)'), Text(0, 0.5, '$\\sqrt{\\sigma}$')]